leetcode挑战：“无重复字符的最长子串”之滑动窗口解决方案

<< 更多leetcode题目

题目链接

https://leetcode.cn/problems/longest-substring-without-repeating-characters/

难度

中等

介绍

在上一篇易水介绍了自己对这个问题的解决方案，但那个方案执行效率和空间使用都很差。本文主要是介绍 stanislav-iablokov 的滑动窗口解决方案，他的算法时间复杂度为 O(n)，空间复杂度为 O(1)，完全可以用"简洁优雅"这四个字来形容！

C++解决方案

class Solution 
{
public:
    int lengthOfLongestSubstring(string s) 
    {
        int max_len = 0;

        // [1] longest substring is the one with the largest 
        //    difference between positions of repeated characters; 
        //    thus, we should create a storage for such positions 
        vector<int> pos(128,0);

        // [2] while iterating through the string (i.e., moving 
        //    the end of the sliding window), we should also 
        //    update the start of the window 
        int start = 0;

        for (int end = 0; end < s.size(); end++)
        {
            auto ch = s[end];

            // [3] get the position for the start of sliding window 
            //    with no other occurences of 'ch' in it 
            start = max(start, pos[ch]);

            // [4] update maximum length 
            max_len = max(max_len, end-start+1);

            // [5] set the position to be used in [3] on next iterations
            pos[ch] = end + 1;
        }

        return max_len;
    }
};

算法分析

stanislav-iablokov的算法，思路正是上一篇中易水提过的想法：最长不重复子串，是两个重复字符之间的最大长度。但当时易水陷入了思维定势，始终想用字符查找、比较解决问题，但没有想到滑动窗口的解决方法。
在此算法中，stanislav-iablokov用 start 表示滑动窗口的起始位置，初始值为 0，后续循环中会将其值设为离起点最远的重复字符所在位置的后面(即其数组下标加1)；end表示滑动窗口的结束位置，初始值为 0，在循环中依次后移；pos[128]数组用于存放每个字母上一次出现过的位置，初始值为0，代表字母没出现过。
在循环中，end会依次后移，然后会检查start是否需要后移：如果出现了重复字符，且重复字符在当前start之后，则将start后移至该重复字符的后面；否则start保持不变。在确定了滑动窗口的起始地址后，计算窗口中字符长度，即为不重复字符的长度，将其最大长度保存至 max_len 变量即可。
算法的精妙之处在于如何确定滑动窗口起始位置：如果在当前start之后存在end位置上的字符，说明在当前start和end间出现了重复字符，此时需要把start后移至重复字符的后面。移动之后，在start和end之间就不存在重复字符了。
另外，这个算法还打破了易水的思维定势，程序中完全没有用到字符查找、字符比较，而是用数组下标代之！
易水画了一副示意图，展示了该算法对于字符串 pwkwew 的处理过程：

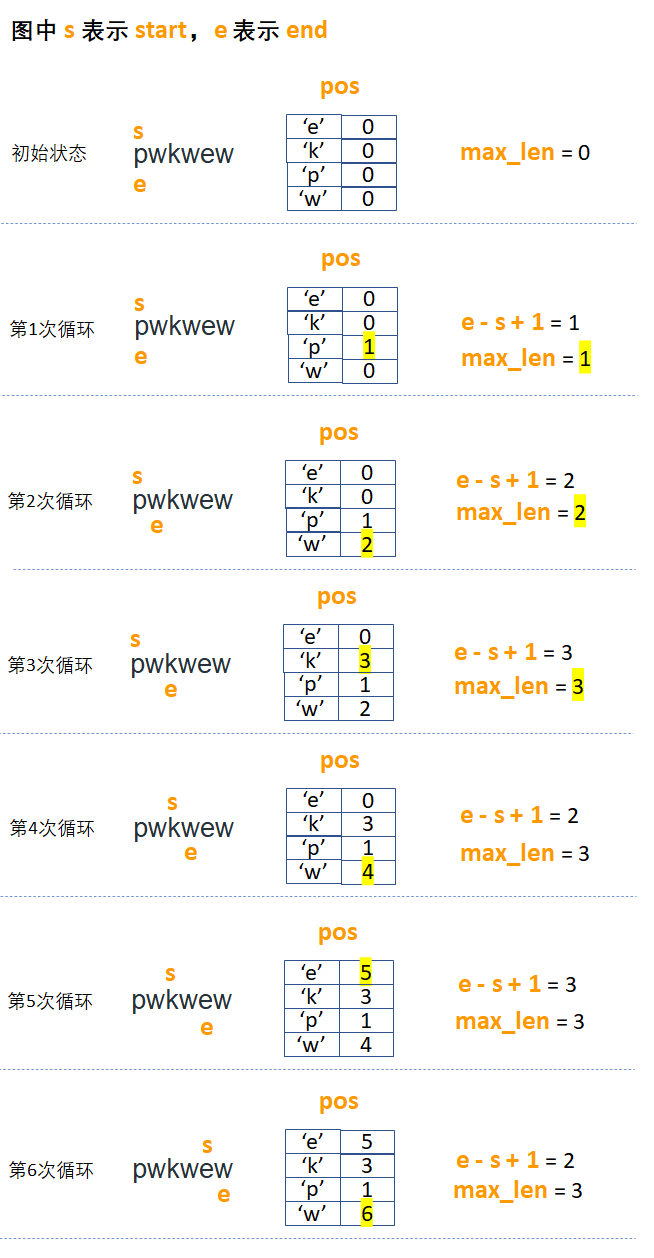
总结

以后在遇到下面这类问题时，可以考虑滑动窗口方案：

• 给定一个序列，例如数组、字符串；
• 需要处理的数据是其中的一个子序列或子字符串；
• 给定了一个固定的窗口大小，或是要求找出窗口的大小(例如本题)；

使用滑动窗口方案，关键在于窗口起点和终点的确定，这需要根据问题进行具体分析。